Background

Linked List vs. Array - search()

Linked lists have a slight downside when it comes to finding an item. If the item we're trying to find is located towards the end, then we'd have to traverse nearly all nodes until it's found. The result is that the search operation in a linked list takes O(N) time.

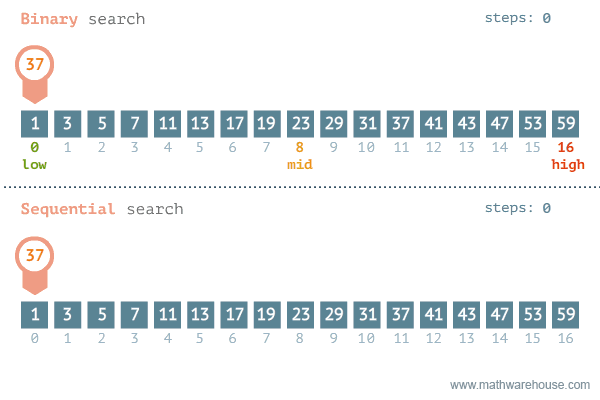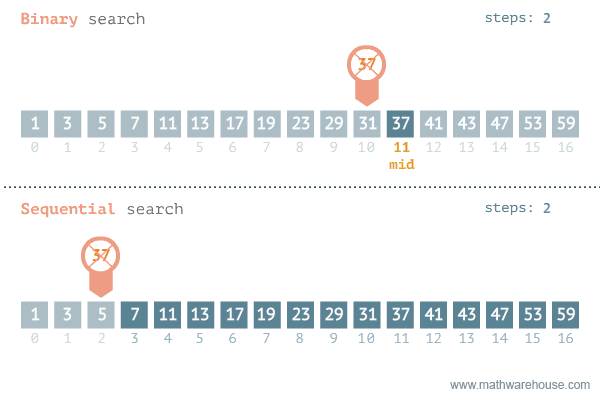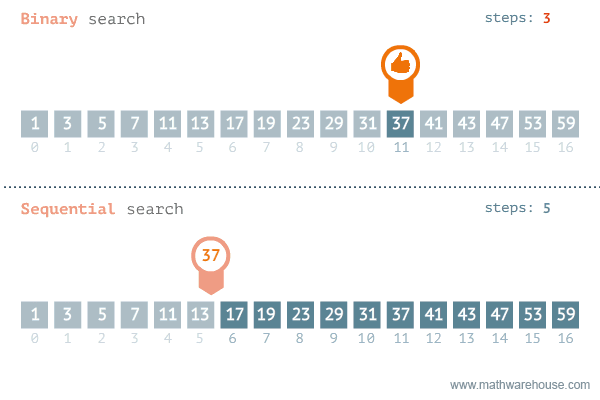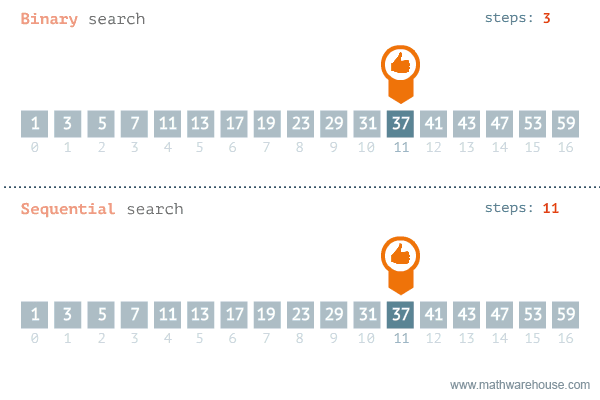
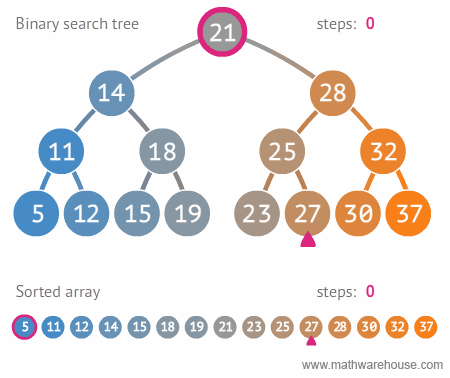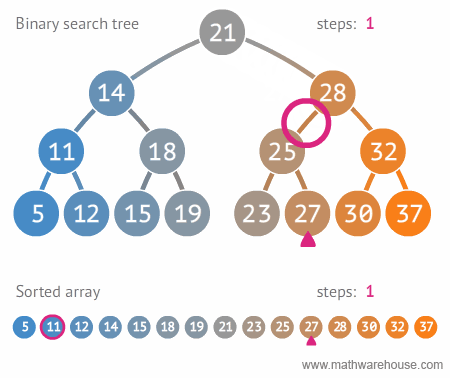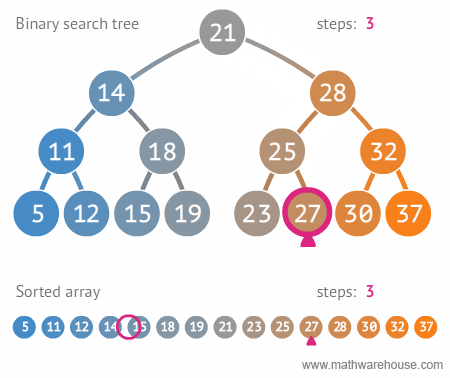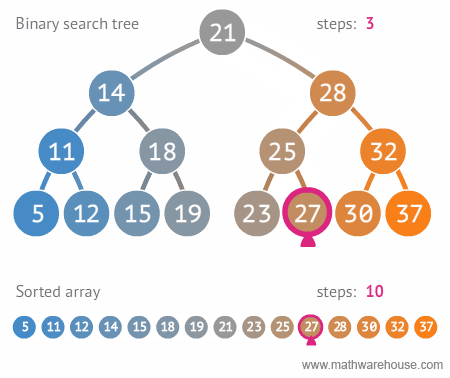
For arrays, we can take a more intuitive approach using Binary Search. Binary Search is a simple algorithm for finding an element in a sorted array. The result of using this method of searching is that the search operation in a sorted array takes O(log N) time.

Binary Search Explanation: We designate a pointer to the middle of the array and check if the number we're trying to find is equal to the middle element. If it is larger, we recursively call the search method on the right half (larger half) of our array. If it is smaller, we do the same process but with the left half of the array. We continue this process until we have found our element or concluded that the element is not in the array.

Sequential vs. Binary Search Visualization

Linked List Optimizations:

1. A pointer to the middle node [1].

2. Flip the nodes' pointers, which allows us to traverse to both the left and right halves [1].

3. Add pointers to the middle of each recursive half [1].

What Makes a Tree?

• nodes that hold data.

• edges that connect those nodes.
  * Constraint: there is only one path between any two nodes [1].

What is a Binary Tree?

A binary tree is inherently a tree, that follows the binary property constraint: where each node has either 0, 1, or 2 children [1].

What is a Binary Search Tree (BST)?

Now that we have the background explained, we can identify what exactly a Binary Search Tree is.

A Binary Search Tree is inherently a binary tree, which maintains the property that...

For every node X in the tree:

• Every key in the left subtree is less than X’s key [1].

• Every key in the right subtree is greater than X’s key [1].

Two Shapes of BST?

"Bushy" BST - This shape forms if we have a full BST. In other words, if each parent node has the maximum number of children (e.g. two children).

• "Spindly" BST - This shape forms if we keep inserting numbers that are greater than our previous node. In this example, we start with the root node 2 and insert 5, 8, 9, 10, 12, 13, 14... (each number inserted is larger than the previously inserted number). This same pattern works if we start with a large root node value and insert subsequently smaller numbers.

  

Time Complexity of BST Operations

Search - O(log N)

Searching for an element in a BST takes O(N) time since in the worst case we would have to search a spindly-shaped BST. Therefore, we need to traverse the entire BST to reach the leaf. The best case would be O(1) if we found the element at the root of the BST.

Insert - O(N)

The time complexity to insert an element in a BST is O(N) since in the worst case we would have a spindly-shaped BST, and would have to traverse the entire BST from the root until we get to the leaf to insert the new value. The average case would rely on the tree having a bushy shape and would be O(log N). The best case would be O(1) in certain circumstances.

Delete - O(N)

Deletion in a BST takes O(N) time. The worst case arises when we need to traverse a spindly-shaped tree to get to the item for deletion which can take O(n) time. Conversely, if the tree is bushy, the best case would be O(log N).

References
[1] https://joshhug.gitbooks.io/hug61b/content/chap10/chap102.html
[2] https://courses.cs.washington.edu/courses/cse373/20wi/assets/images/readings/